
Binomial Probability Table N 13. Suppose the number of TVs in a household has a binomial distribution with parameters n 23 and p 40. For failure the probabilty is 1 p the probability of getting r successes out of a total trial of n events ie. PROBABILITY TABLES Individual probabilities for the Binomial Distribution The table gives the probabilities PX x where X Binnp. N13 0 08775 05133 02542 01209 00550 00238 00097 00037 00013 00004 00001 13 1 01152 03512 03672 02774 01787 01029 00540 00259 00113 00045 00016 12 2 00070 01109 02448 02937 02680 02059 01388 00836 00453 00220 00095 11.
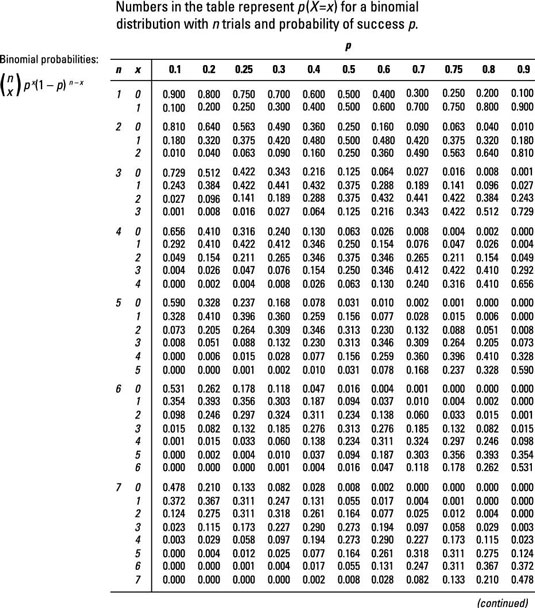
P Probability of Success in a single experiment. The probabilities in each are rounded to three decimal places. P xnp n C x p x 1-p n-x. The sum of the probabilities in this table will always be 1. Computations are rounded off at the third decimal place n 5 p k 01 05 10 20 30 40 50 60 70 80 90 95 99. These are also known as Bernoulli trials and thus a Binomial distribution is the result of a sequence of Bernoulli trials.
The binomial distribution which gives the probabilities for the values of this type of variable is completely determined by two parameters.
With n13 and p07 find the binomial probability P9by using a binomial probability table. The cumulative binomial probability table tells us that finding P X 3 06482 and P X 2 03980. P xnp n C x p x q n-x. The binomial distribution XBinnp is a probability distribution which results from the number of events in a sequence of n independent experiments with a binary Boolean outcome. PROBABILITY TABLES Individual probabilities for the Binomial Distribution The table gives the probabilities PX x where X Binnp. If we perform a large number of independent binomial experiments each with n 10 trials and p 75 then the average number of Ss per experiment will be close to 75.