
Confidence Interval For Binomial Distribution. Suppose n is the sample size r the number of count of interested outcome and p r n is so called binomial proportion sample proportion. We do n 500 attempts and get x 62. We want to create a confidence interval I p for p. The most common method is based on the normal approximation the Agresti-Coull method HELP AGRESTI COULL for details In most cases this is the recommended method to use.
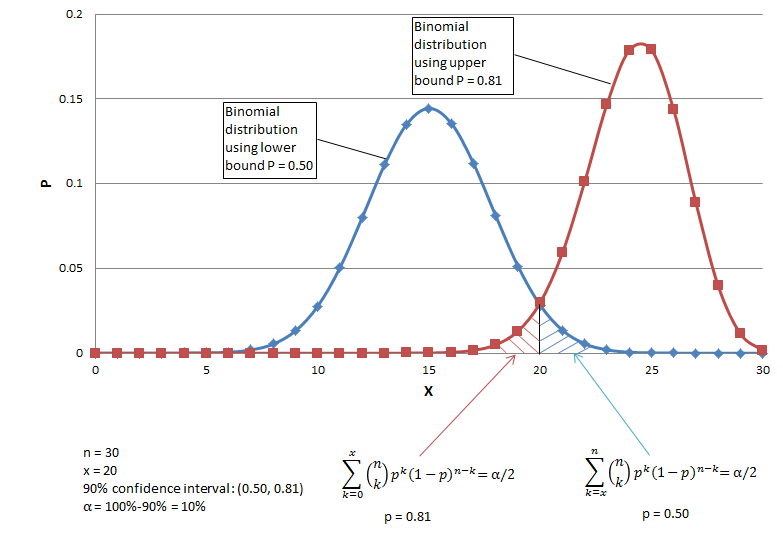
A confidence interval CI is a range of values computed from the sample which is with probability of 95 to cover the population proportion π well you may use any pre-specified probabilities but 95 is the most common one. Which is based on the exact binomial distribution and not a large sample normal approximation as is the Wald method. Studies have shown however that this confidence interval is very conservative having coverage levels as high as 99 for a 95 CI and requiring significantly larger sample sizes for the same level of precision123. Suppose that X is B i n n p. A confidence interval for a binomial probability is calculated using the following formula. Binomial Probability Confidence Interval Calculator.
Please enter the necessary parameter values and then click Calculate.
An exact method based on the binomial distribution. Suppose that X is B i n n p. N p 5 and n 1 p 5 the confidence interval can be estimated by a normal distribution and the confidence interval constructed thus. If the average p is not near 1 or 0 and sample size n is sufficiently large ie. This calculator relies on the Clopper-Pearson exact method. Confidence Interval p - z p 1-p n.