Geometric Mean Annual Return. To calculate the geometric mean return we follow the steps outlined below. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature such as a set of growth figures. Geometric mean is also utilized in research on cell division and bacterial development among other things. The trick is to avoid problems posed by negative values.
Geometric Mean Return Formula. Example of the Geometric Mean Return Formula. Given a series of annual percentage returns find the average return using the geometric mean. The annual rate of return formula is calculated as a geometric mean that represents what an investor will earn over a period of time if the annual rates of return are combined. Definition of Geometric Average Return. The geometric mean return formula is a way to calculate the average rate of return per period on investment that is compounded over multiple periods.
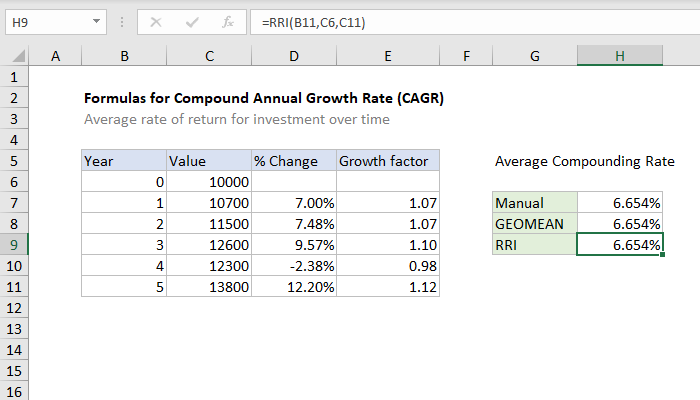
You want to know the annual geometric return.
It would be incorrect to use the arithmetic mean of adding the rates together and dividing them by three. Geometric mean is also utilized in research on cell division and bacterial development among other things. Finally subtract 1 from the final result. Definition of Geometric Average Return. Geometric mean is used in finance to calculate average growth rates commonly known as compounded annual growth rates. Because many of the value line indexes which is used by financial departments use GM.
